Connaissez-vous Set! ?

Cet article vous a plu ? Pourquoi ne pas le partager ?

J’adore les jeux simples qui s’appuient sur des fondamentaux mathématiques plus poussés, en général d’ordre combinatoire. Après le Sudoku ou Dobble, je vous propose de découvrir Set! Ce jeu est sorti de l’esprit de Marsha Falco, une chercheuse en génétique, qui cherchait à illustrer de manière visuelle les problèmes d’hérédité sur lesquels elle était amenée à travailler. En transposant son sujet par écrit sur des petites cartes colorées, elle en a tiré ce jeu original, accessible à tous, mais dont les limites font appel à une gymnastique intellectuelle plus poussée.

Set! se présente sous la forme d’un jeu de 81 cartes qui représentent des figures. Chaque figure possède un à trois symboles identiques, qui peut être bleu, rouge ou vert, plein, vide ou quadrillé. Trois symboles sont utilisés: le losange, une sorte de forme ovale et une sorte de S. En tout, il existe donc 4 caractères ternaires, ce qui détermine donc 3^4, soit 81 cartes différentes.

On commence par étaler 12 cartes au hasard. Le but du jeu est de composer des « Sets », c’est à dire des triplets de cartes qui répondent à la règle suivante: si l’un des caractères apparaît sur deux des cartes, il doit aussi apparaître sur la troisième. Ainsi, dans le triplet qu’on doit former, les trois cartes doivent avoir la même couleur ou des couleurs différentes deux à deux. Et ainsi de suite sur les quatre autres critères. Si auc tel triplet n’est possible, on pose trois cartes supplémentaires prises dans le talon et on continue.

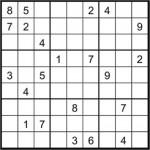
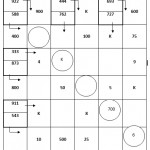
Sur le plateau ci-dessus, on peut ainsi former un Set! avec les trois S verts pleins, mais aussi avec les trois cartes à gauche, avec le losange rouge, les deux S vert et les trois carreaux violets, etc. C’est très simple, très visuel, à la portée d’un enfant de sept ou huit ans.

Mais si on creuse un peu, plusieurs questions se posent, dont les réponses sont plus ou moins faciles à trouver.

• Combien peut-on former de Set! à partir de deux cartes données? La réponse est un et un seul set: cette carte est formée en adoptant le même critère commun s’il existe, et en complétant au troisième pour les autres critères.
• Y a-t-il toujours un Set! possible lorsqu’on retourne 12 cartes? La réponse est non. Vous le constaterez aisément au bout de quelques parties.
• Quelle est la probabilité de tomber sur une distribution de 12 cartes sans Set! ? Je n’ai pas la réponse.
• Quelle est la plus grande distribution de cartes sans Set! ? Wikipedia parle de 20 cartes, avec une probabilité très proche de 0 (à 10^(-19) près). Mais là aussi, sans démonstration.

J’ai écrit un petit programme python de 200 lignes qui simule une partie de Set! et donne toutes les solutions possibles à chaque étape du jeu. Je le tiens à la disposition des joueurs qui aimeraient creuser le sujet…

Cet article vous a plu ? Pourquoi ne pas le partager ?